Materials Scientists and Mathematicians Challenge Central Hypothesis in Grain Growth Modelling for Thin Films
The recently published manuscript by Professor Katayun Barmak (Department of Applied Physics and Applied Mathematics, Columbia University), Professor Yekaterina Epshteyn (Department of Mathematics, University of Utah), and graduate student Matthew Patrick (Department of Applied Physics and Applied Mathematics, Columbia University) [M. Patrick et al., Acta Materialia 242 (2023) 118476] challenges the commonly used assumption that grain growth in thin films is governed by a force balance at grain triple junctions known as the Herring equation, where geometries are determined by boundary energy anisotropy alone. These novel experimental findings could lead to a significant reformulation of existing grain growth models.
The vast majority of metals and alloys used in engineering applications, from structural components to microchip interconnects, are polycrystalline in nature. This means that they are composed of many small crystals, each made of an identical material, but with their atoms arranged in lattices of different orientations. These small crystals join together at planar defects known as grain boundaries. The grain and grain boundary structure of materials has a profound impact on their properties and performance, from ductility to electrical resistivity, and so an understanding of how their structure evolves in time is a critical tool in designing the next generation of materials.
Grain boundaries are non-equilibrium defects that have some associated excess energy (GBED) which is a function of their crystallographic character (GBCD). These boundaries meet at points known as triple junctions. It has long been accepted that the angles between boundaries at these junctions are dominantly determined by a force balance known as the Herring equation, where the forces are assumed to be proportional to the energies associated with each boundary. This can be thought of as analogous to tensions in three wires, joined at a single point. A tighter tension (higher boundary energy) would be associated with a more acute dihedral angle. This idea has been incorporated into many theoretical models of microstructural evolution. It has also been used to experimentally determine relative energies of boundaries in bulk materials by measuring the angles at the triple junctions of boundaries with known crystallographic character and then solving the Herring equation. This method has been applied to a variety of metals and ceramics, showing strong agreements with theoretical boundary energies calculated using molecular dynamics (MD), and revealing a strong inverse correlation between populations of boundaries and their associated energies.
In the thin metallic films examined in the new work, the GBCDs exhibited inverse correlations with the MD-computed energy distributions, indicating that the systems are selecting the lowest energy boundaries as expected. Surprisingly, however, when the geometries at triple junctions were used to solve the Herring equation, the relative energies did not inversely correlate with populations of grain boundaries and did not correlate with theoretical energies. Thus, in these spatially constrained systems, the conventional Herring equation cannot be used to describe the system’s behavior, since the GBED should be dependent only on the material in question. It follows that the evolution of the microstructure of these materials, and in particular the geometry of triple junctions, are governed by a more complex interplay of factors that might include surface energies, strain energies, and other energy reduction pathways which drive the formation and evolution of the materials’ structure.
The new findings come at a time when other widely employed assumptions about grain boundary behavior including bedrock models like curvature-driven grain growth, are being re-examined. The behavior of triple junctions is of increasing interest to the grain-growth modeling community, given that these features are convenient microstructural markers, and so the energetic and kinetic factors dictating junction dynamics are highly relevant. By challenging an important assumption about grain growth, this paper advances the study of grain boundary network structure and its evolution and invites the development of more predictive models to help unravel some of the mysteries of grain growth.
Barmak and Epshteyn’s research was funded by the Division of Mathematical Science and the Division of Materials Research of the National Science Foundation.
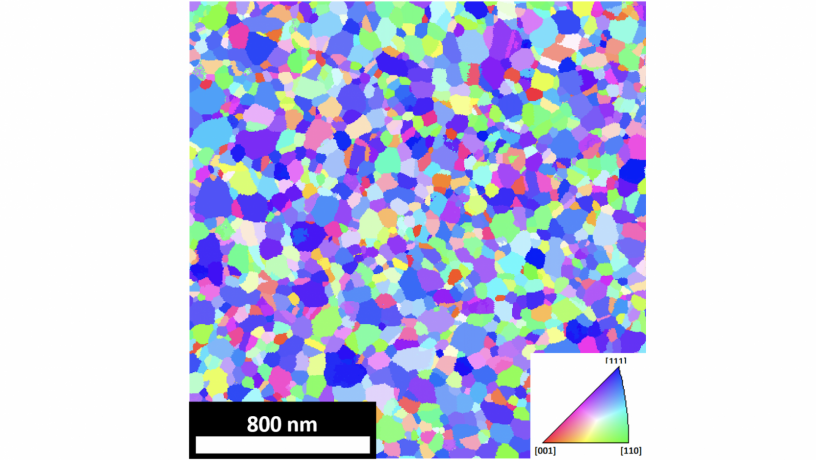
Crystal orientation map of an aluminum thin film in the sample normal direction. The orientation key is given on the right and is labelled with the Miller indices of three crystal directions at its corners.